
排列组合a和c的区别 排列组合的区别排列组合的区别排列与组合的共同点是从n个不同的元素中,任取m(m≤n)个元素,而不同点是排列是按照一定的顺序排成一 排列组合公式 排列组合中怎样区分排列与组合的使用排列是考虑顺序的,即同样的元素顺序不同是不同

知道了这个过程,算法也就写出来了: 将数组看为一个集合,将集合分为两部分:0~s和s~e,其中0~s表示已经选出来的元素,而s~e表示还没有选择的元素. 顺序从 中选出一个元素与 交换(即选出一个元素) 共6个,即3!=3 这个是怎

以此类推,把所有可能的情况取一遍,就是全排列了,如图: 然后再从剩下的集合中取出一个元素,例如取出2,那么还剩下{3}. 首先取一个元素,例如取出了1,那么就还剩下{2, 3}. 这个是怎么算出来的呢? 共6个,即3!=3*2*1=6.

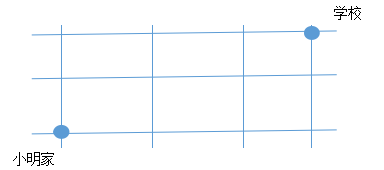
解析:先确定行走方向与路径(如图),分析这道题小明可从家直接到达A点和B点,而C点不能从家直接到达,必须先走到A点或B点后才能到达C点,因此这道题的标点顺序必须先标A点和B点后才能标出C点,其他点标数顺序以此类推.A点和B点都只能从家来,所以A点和B点都只

m)/m!=n!/m!(n-m)!. n个元素被分成k类,每类的个数分别是n1,n2,...nk这n个元素的全排列数为 n!/(n1!*n2!*...*nk!). k类元素,每类的个数无限,从中取出m个元素的组合数为C(m+k-1,m).

执行结果:


求排列组合A,C的计算方式(图9) 求排列组合A,C的计算方式(图11) 求排列组合A,C的计算方式(图14) 求排列组合A,C的计算方式(图17) 为了解决用户可能碰到关于\"求排列组合A,C的计算方式\"相关的问题,突袭网经过收集整理为用户
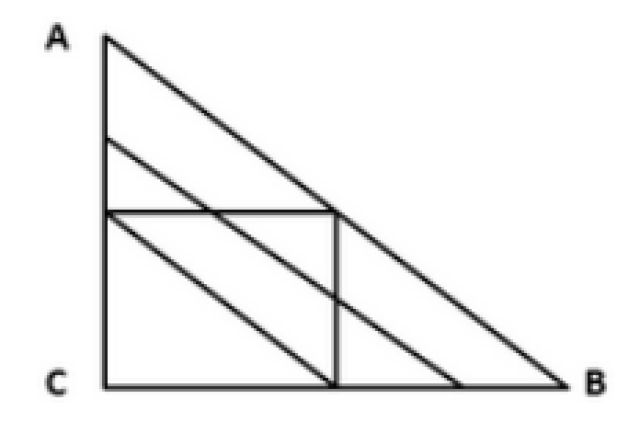
【例3】从A地到B地的道路如图所示,所有转弯均为直角,问如果要以最短距离从A地到达B地,有多少种不同的走法可以选择? C.20种 D.10种 【例2】A、B、C三地的地图如下图所示,其中A在C正北,B在C正东,连线处为道路.如要从A地到达B地,

一、排列与组合的概念 对于排列和组合最重要是要区分两者的不同,排列是有顺序要求的,而组合是无顺序要求的.说起来简单,但是很多同学在做题的过程中还是会搞混,分不清是用组合C还是用排列A(P).有一个简单的方法,同学们可以拿来应用以作区分:交换两个元素的位



关键字:排列,组合问题的典型方法 一.排除法 例1:(2008年四川卷)从包括甲、乙共10人中选4人去参加公益活动,要求甲、乙至少有1人参加,则不同的选法有( ) 解析:审题后针对题目中的至少二字,首选排除法. .选C.
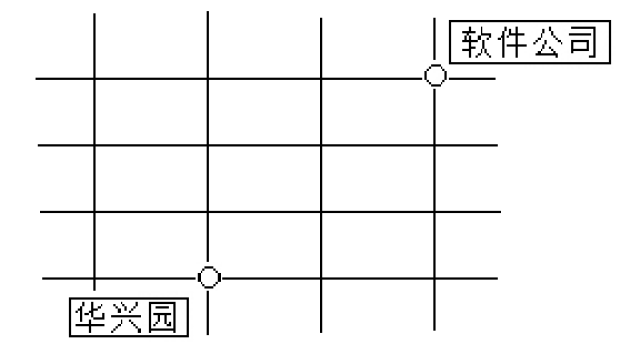
A.12种 B.15种 C.20种 题干特征:给定几何图形,已知起点终点、运动方向,求从起点到终点的不同走法数 方法技巧:见视频~ 【例1】小张从华兴园到软件公司上班要经过多条街道(软件公司在华兴园的东北方).假如他只能向东或者向北行走


备战2017高考高三数学(理)全国各地二模金卷分项解析:专题12 排列组合、二项式定理 【备战2017高考高三数学全国各地二模试卷分项精品】专题 排列组合、二项式定理一、选择题1.【2017安徽阜阳二模】的展开式的常数项是( )A. B. C. D.

这道题应该在排列组合中算得上是一道比较费解,且抽象的题了.楼主不用太多着急,慢慢理解,这里所刻画地C(8.3)的意义. 祝学业有成~ 补充: 补充:楼主不必纠结于为什么要选这8个点,相反可以把思路多定格在由这8个点所确定的唯一的质点运动路径.这

在2k步时位于原点的走法是C(2k,k),而我们要求的一直>=0的走法数目.大致的思路是翻折,如上图所示,如果之前已经金身不保,把后面的走法统统对调,向左走变向右走,向右走变向左走...则走法为C(2k,k-1)种,则金身不破的走法有C(2k,k)-C(2

网友:汤煜杭:闭关会很久。
网友:孟因熊:东伯大人!”公良远直接道。
网友:陈谋:一道道身影接连出现。
网友:张谱辈:最后死在了梵子齐楠手上。
网友:郭淦两:一看就是一行飘逸的字体,字形非常优美,看得出宁英的大气与潇洒,奈何韩云笙愣是一个字都看不懂。
网友:方毫骀:是源自于‘断牙山脉’。
网友:罗夕论:他起身郑重拜谢元湛的款待,而后决绝起身而去。




