
则角动量守恒表明行星轨道必在一平面上.矢径在相等的时间内扫过的面积相等,这就是开普勒行星运动三定律(见开普勒定律)之一. 一孤立质点系统,如不受外力或外界场的作用,质点之间的内力服从牛顿第三定律(见牛顿运动定律ij=-ij(图2).内力系对固定点的主矩

碰撞之前,系统对于定轴0的角动量为2mvL 由于是完全非弹性碰撞,即角动量守恒:2mvL=Jω,(其中,J是该系统的转动惯量为1/3mL2+mL2+mL2) 因此得到ω=6v/7L 过程如下图:


请问我们的质疑是否有漏洞?答案是否有问题?求高手指点,回答好有加分. (注:题目摘自《高中物理竞赛培优教程》第五章第二节,解析摘自《高中物理竞赛培优教程习题全解》) 1.选取的参考系为 杆的中点 ,但碰撞过程中该参考点做过加速运动,系非惯性




物理动量守恒与动能守恒的公式(图18) 为了解决用户可能碰到关于\"物理动量守恒与动能守恒的公式\"相关的问题,突袭网经过收集整理为用户提供相关的解决办法,请注意,解决办法仅供参考,不代表本网同意其意见,如有任何问题请与本网联系. 物理动量守恒与动能守


EXL-4角动量守恒演示仪用于定性观察合外力为零的条件下,提的角动量守恒.

首先在棒无初速度释放后到与球碰撞前,只有重力对棒做功,所以棒的机械能守恒,mgl/2=转动惯量*角速度平方/2 而棒绕一段转动的转动惯量=m*l/3 所以此时角速度可求
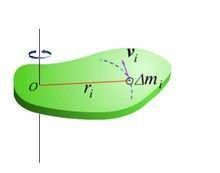
力矩 始终等于零的 质点 和 质点系 围绕该点


追问: 追答: 那些符号我实在是不知怎么打出来,请谅解,w表示角速度,I 表示转动惯量, 整个解答都是从角动量守恒出发的.解答应该是没问题的,我遇到的一题与这相似如图、、、、、当然算出的是相对绳子的速度,速度加减自己应该可以搞定了吧

角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 篇二 : 角动量守恒定律 角动量守恒

相应表达式: 若 =0, L=r*P=恒矢量. 则 r 这就是角动量守恒定律. 可以看出角动量守恒定律成立的条件是质点 所受的合外力矩为零, 即 =r*F=0.此条件实现有两种可能: r 一是合外力为零, 二是可能外力 但是它不受牛顿

一是合外力为零, 二是可能外力 ≠O,但力的方向与力的作用点相对于参考系 O 角动量守恒定律的应用 O 的失径在同一直线上,即与其夹角为 0,也就是 =0,故力矩为零. 对于守恒量 L 为恒矢量表示角动量的大小 rmvsin 无一相


角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 角动量守恒定律 篇三 : 浅谈角动量守恒定律 摘 要:角动量守恒定律与动量守恒定律及对一轴线和对轴线上任一点的角动量守恒两个容易混淆的问题,从守恒条件和守恒量两

量子力学中,中心力场,动量是守恒量不?:并不是守恒量. 中心力场下,力学量完全集一般选择能量,角动量和z方向的角动量. 量子力学中,[l,s·l]≠0,从而说明轨道角动量和自旋角动量都不守恒.为什么?: [l,s·l]≠0?如你所说应该是等于0啊! 但
网友:周势:抓了也难驯服。
网友:胡韵:它就像你我和普通人的区别一样,只有这样的灵药才能提供我消耗。
网友:董玻敖:你回答我你外公和外婆都叫什么名字,我在你小时候和你说过的,你一定不会忘记的。
网友:魏薏:可以和特殊者相提并论的他们在这个“奴隶主”说话如此难听之后,居然全部一言不发,一双眼睛只紧紧盯着地面,心脏却跳得很快,好像面对这个面具人头头相当紧张似的。
网友:蒋见永:林拾音便主动请缨替韩云笙缠绷带,她的动作轻缓,一举一动都很小心翼翼,生怕弄痛了韩云笙。
网友:刘斟樟:此时仍然没有好转。
网友:孙问礼:只要莲川木汐借以墨遁构造出相同的构造,便可以再度使用,倒也没有多大的影响。
网友:余通:莲川木汐写下最后一个符文,看着写满了文字、数字、符文的卷轴,莲川木汐不由得吐出了一口气,终于是把墨遁开发事宜相应的计算和推导进行完毕了,自从回来之后,莲川木汐一直深居简出的研究了大半个月,终于是给墨遁的开发初步制定出了一个方向和大致的规划。
网友:孙测堆:正面向着墨龙撞去,顿时猛烈的寒风和碎冰向着四面八方扩散开来,墨龙和白鸟的争斗,使得整个训练室由夏日变成了冬季,寒风呼啸,碎冰飞雪四处飞舞,眨眼之间气温降低到了极为惊人的程度,整个训练室已经被白雪和冰层尽数覆盖!
|
|
- 上一篇:寒暄意思 寒暄和寒暄的区别_寒暄里面的寒暄解释为什么
- 下一篇:返回列表






