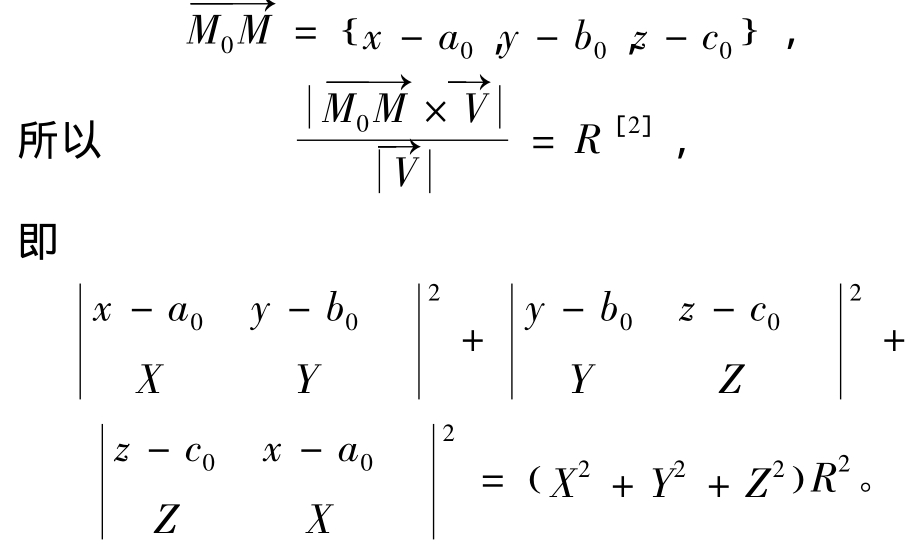
命题3 准线 再设点M(x,y,z)是圆柱面上任一点,则有





热心网友
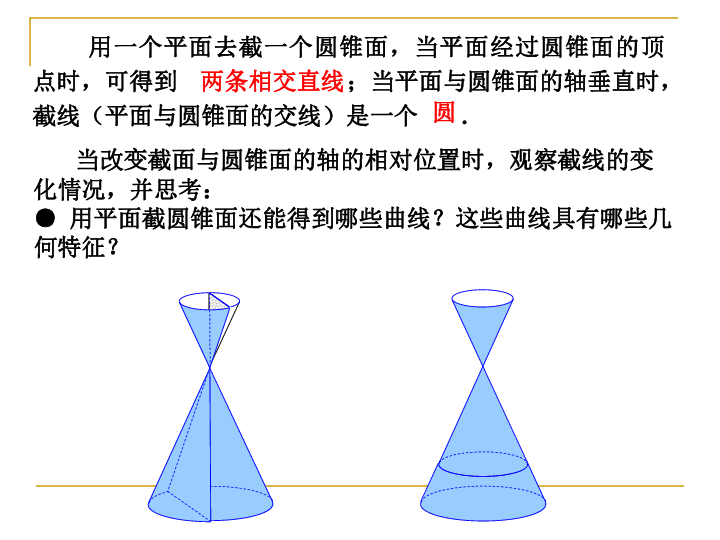
2.1.1椭圆及其标准方程 ==================资料简介======================新人教A版选修1-1 文科 2.1椭圆新授课课件(本课件共有24张幻灯片)用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到 ;

返回《高等数学专题讲解目录》 一些曲面的球面坐标方程 球面坐标适合描述球面、圆锥面等曲面,具体情况如下:

2.1.1椭圆及其标准方程 ==================资料简介======================新人教A版选修1-1 文科 2.1椭圆新授课课件(本课件共有24张幻灯片)用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到 ;
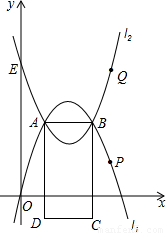
,直接写出b的取值范围.

代入(式三)得:l=0;c+d+e+f=0..............即 f=-(c+d+e) 因此,包含x轴,y轴及直线x=y=z的圆锥面方程为: (比如,最简单的一个是 z^2 = xy,图像是无限椭圆锥面)

(4)顶点在 ,开口朝下的下半个圆锥.

因为xy+yz+zx=0,即0.5*((x+y+z)^2-(x^2+y^2+z^2))=0,即(x+y+z)^2=x^2+y^2+z^2. 因此,考虑(x,y,z)和向量(1,1,1)的夹角,由定义,夹角的cos值为 xy+yz+zx=0,得z=

OpenCASCADE中圆锥面的参数方程为: 可知圆锥曲面与圆柱曲面一样,都是在u方向有界,在v方向无界.对其进行裁剪生成拓朴面并显示pcurve的Tcl脚本如下所示: 生成结果如下图所示: 由上图根据pcurve的着色规则可知,圆柱面的pcu

解答: 答案:不一样. 原因:椭圆锥面与圆锥面是锥面的不同形态. 椭圆锥面的方程是(x/a)2+(y/b)2-(z/c)2=0.当a=b时,即为圆锥面.

式中: .将式(3)和式(7)代入式(9)可可获得超椭圆描述的空间圆锥壳面上开孔边界的参数方程. 上述回转壳开孔边界的参数方程仅由少数几个平面超椭圆参数变量描述,通过修改平面超椭圆参数变量,就可以实现回转壳开孔形状的改变,为回转壳开孔形状优化提供了

扩展资料: 抛物线是指平面内到一个定点(焦点)和一条定直线(准线)距离相等的点的轨迹.它有许多表示方法,例如参数表示,标准方程表示等等. 它在几何光学和力学中有重要的用处. 抛物线也是圆锥曲线的一种,即圆锥面与平行于某条母线的平面相截而得的曲线.抛

凸轮毛坯每转一周,刀具再作一次沿自身轴线方向的进给运动,即可以逐步完成对凸轮廓面的加工.如果没有与圆锥滚子尺寸相同的刀具,也可采用尺寸小于圆锥滚子尺寸的刀具加工凸轮廓面.但在该种情况下,必须预先确定刀具轨迹.图3示意用锥形铣刀加工曲面的情况.刀头部最小半径
网友:张骀侏:同时摇头,“当初东伯兄和红魔神帝那一战你是没看到,虽然外界盛传东伯兄击败了红魔神帝,可详细战斗情形,知道者却极少极少。
网友:钟炳呗:用剑尖刺穿韩谷轩身上的几个穴位,更甚至还轻描淡写地用剑尖在韩谷轩脖子上开了个狰狞的血口,且将剑尖再度递入韩谷轩的心口,往内捅了一通。
网友:姚司:远处九蛇战船的舱门飞出来一名金袍男子,是颇为霸气的男子,眼眸中隐隐有着煞气,只见他一挥手就收起了九蛇战船。
网友:徐磬:这种压制渐渐失效,大吞噬术却没能找到目标,那么又缺乏自己停止施展能力的这个人体内运行的功法便只能吞噬他自己。
网友:汤治鲤:但别人听久了,就难有新鲜之感。
网友:孙瑞侣:就只好直奔眼下情况的重点。
网友:郝凸呢:我乃是实话,混沌境以下,讲道敢和东伯长老比的可没几个。
网友:龚史仔:便是十万亿年便可能成究极吧,我必须在十万亿年内成功。
|
|
- 上一篇:机甲星球 机甲星球在线阅读_机甲星球免费阅读最新
- 下一篇:返回列表





