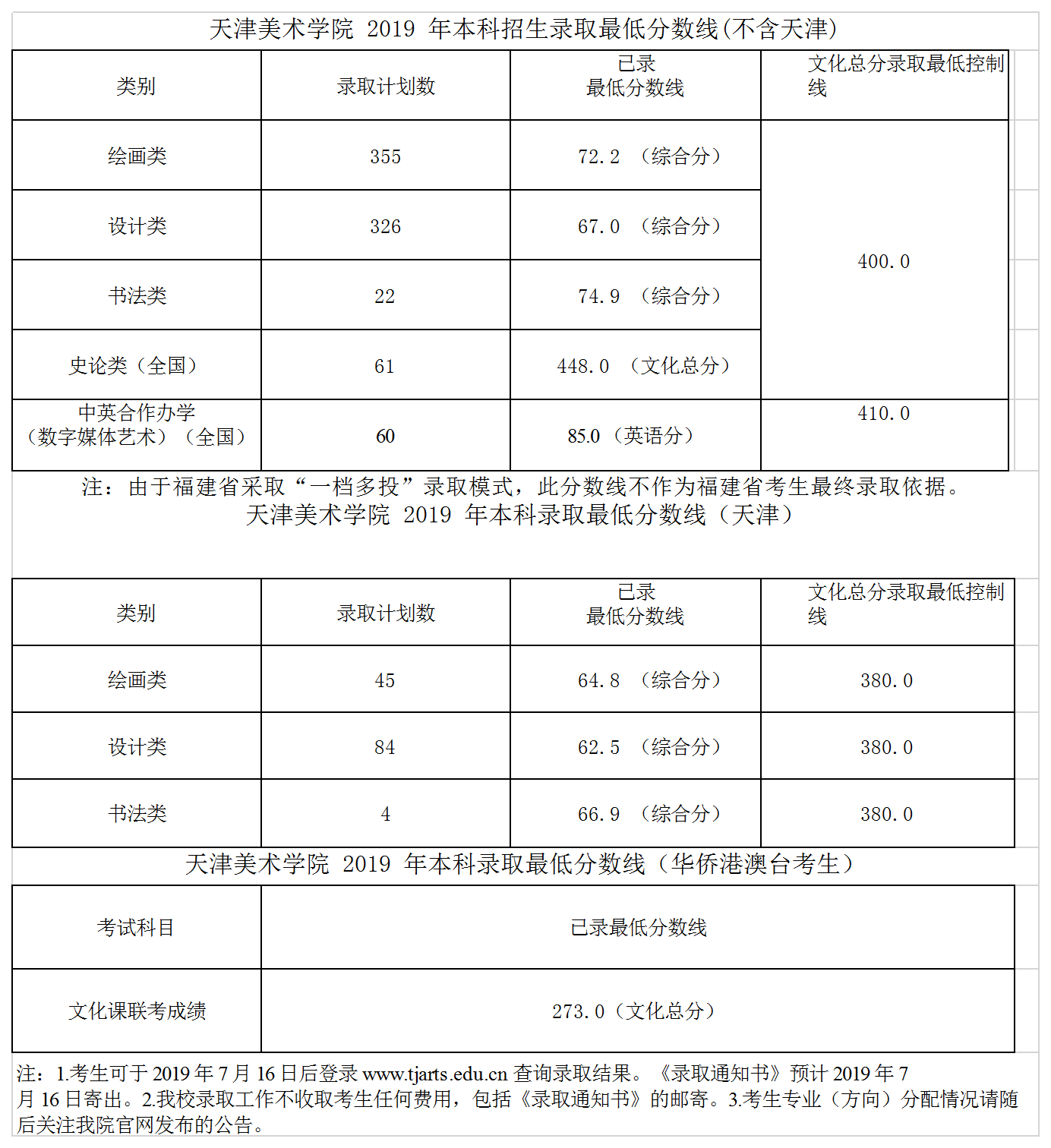
答:性质; 2.2 抛物线的简单性质(图22) [学习目标] 1.通过图形理解抛物线的对称性、范围、顶点等简单性质. 2.掌握抛物线的四种位置及相应的焦点坐标和准线方程. 3.能够运用一元二次方程的根的性质解决直线与抛物线的位置关系等问

抛物线 教案 ==================资料简介======================知识梳理:1抛物线的定义,标准方程, 2抛物线的几何性质 3直线与抛物线的位置关系二、新课讲授:(一) 定义:(学生理解椭圆双曲线第二定义提问学生,由
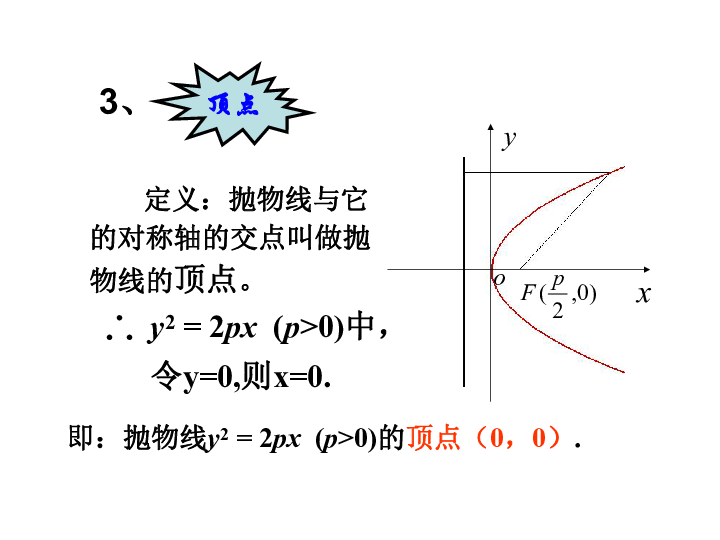
抛物线几何性质 2.3.2.1抛物线的简单几何性质(1)
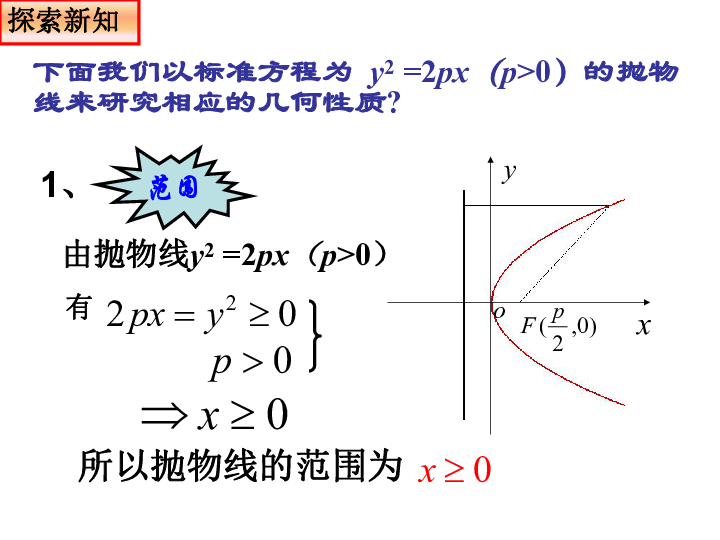
抛物线几何性质 2.3.2.1抛物线的简单几何性质(1)
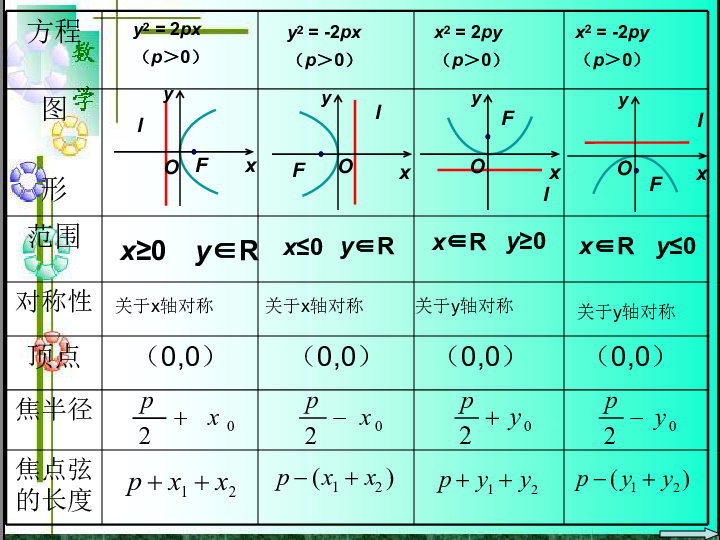
抛物线的简单几何性质 ==================资料简介======================抛物线的简单几何性质 ================================================压缩包内容:数学精华课件
抛物线的几何性质 ==================资料简介======================抛物线的几何性质 ================================================压缩包内容:抛物线的几何性质.p


高中数学:抛物线的几何性质

高中数学:抛物线的几何性质

二·脑洞 本题考查抛物线的焦点弦性质,涉及直线的方程、直线与抛物线的位置关系,平面向量的数量积等知识点,考查数形结合的思想和设而不求的思想,属于中档题. 法1,韦达定理.反设直线方程,这样可以避免斜率不存在时的套路,也使得计算更为简洁;然后联立方程

第二章 2.4.2 抛物线的简单几何性质 =========压缩包内容:第二章 2.4.2 抛物线的简单几何性质 .ppt

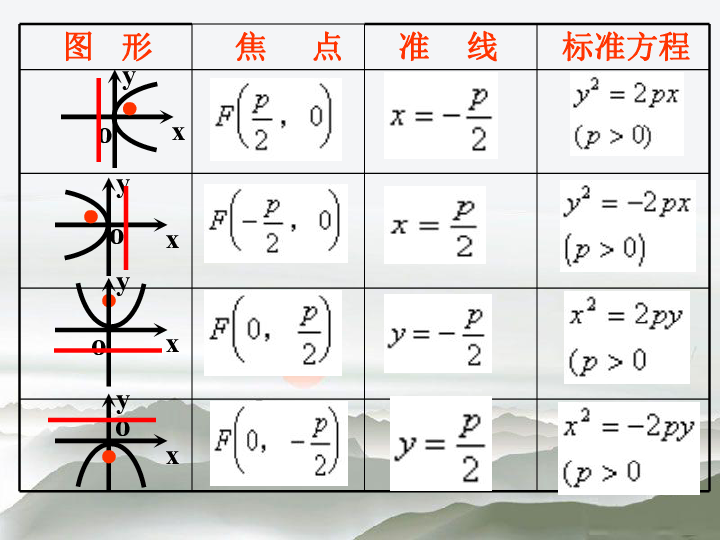
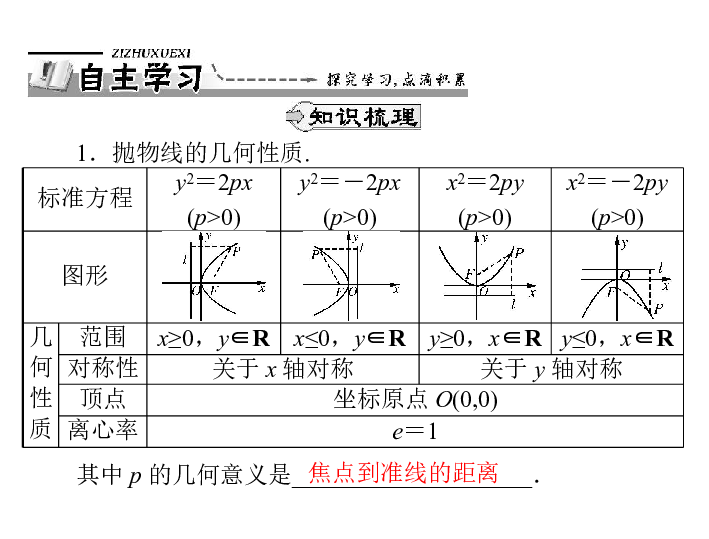
2.4.2抛物线的几何性质 中国人民大学附属中学2.4.2抛物线的几何性质 我们根据抛物线的标准方程y2=2px (p>0) 来研究它的一些几何性质.1.范围: 因为p>0,由方程可知,这条抛物线上任意一点M的坐标(x,y)满足不等式x≥0,所以这条抛

数学:《抛物线的性质》课件(北师大版)


这是抛物线的一条重要性质,尽管这条性质很多同学比较熟悉.但是这条性质的精彩之处在于它既是抛物线的一个\"传统\"性质,又是一个\"经典\"的结论.所以很受各类命题人员(特别是高考命题人员) 的青睐,很多高考试题是以此性质为切入点进行编拟的. 一、抛物线某条重要

(2)把\"数\"、\"方程\"向\"形\"的方向转化,运用运动变化的观点和几何的方法进行研究比直接代数化更简洁. 类型二 抛物线类型题剖析 类型一 抛物线的定义及标准方程的应用


2.3.2 抛物线的简单几何性质 课件3 2.3.2 抛物线的几何性质 前面我们已学过椭圆与双曲线的几何性质,它们都是通过标准方程的形式研究的,现在请大家想想抛物线的标准方程、图形、焦点及准线是什么?

网友:薛蟹蔼:“我现在三重境,算达到‘真也是虚’的地步,而只有达到虚界神心境,才能算是‘虚也是真’。
网友:周客:苏河看了一眼,心中便已然明白,凌空一指点出之后,只见一道绿光惨叫一声,从唐夫人的眉心飞了出来,苏河手指一夹,便将那绿光抓住了。
网友:杨尽:城中灯火熠熠,一片市井繁荣。
网友:朱冲诤:阿婉的荷包也鼓了起来。
网友:陈兀: 韩云笙眼睛一动不动地看着半开的门内,她分明什么都没看到,却似乎已经越过那木门,锁定了韩谷轩这个,天定的主角。
- 上一篇:创造性思维的特点 创造性思维的五大特点_举例说明创造性思维的特点
- 下一篇:返回列表