
奇延拓的图形: 偶延拓的图形: 奇延拓:F(x)=f(x) (当0<=x<=Pi),F(x)= -f(-x) (当-Pi<=x<0); 偶延拓:G(x)=f(x) (当0<=x<=Pi),G(x)= f(-x) (当-Pi<=x<0). 图

偶延拓的图形: 奇延拓:F(x)=f(x) (当0<=x<=Pi),F(x)= -f(-x) (当-Pi<=x<0); 偶延拓:G(x)=f(x) (当0<=x<=Pi),G(x)= f(-x) (当-Pi<=x<0). 图形如下: f(x

奇延拓:F(x)=f(x) (当0<=x<=Pi),F(x)= -f(-x) (当-Pi<=x<0); 偶延拓:G(x)=f(x) (当0<=x<=Pi),G(x)= f(-x) (当-Pi<=x<0). 图形如下: f(x)的图形: 奇延

友情提示:楼主以后问这种理科类的问题不知可否不要在语言类上提问,这样会阻碍楼主得到满意答案的哦! 追问: 哦,那实际情况是不是这样:当获得一个不完整周期信号后,因无法判断其奇偶性,故同时进行\"奇延拓\"与\"偶延拓\",然后,再将\"延拓\"的结果与实际信号

友情提示:楼主以后问这种理科类的问题不知可否不要在语言类上提问,这样会阻碍楼主得到满意答案的哦! 追问: 哦,那实际情况是不是这样:当获得一个不完整周期信号后,因无法判断其奇偶性,故同时进行\"奇延拓\"与\"偶延拓\",然后,再将\"延拓\"的结果与实际信号




黎曼函数是(s)在整个复平面的解析延拓,将s的定义域扩展到整个复平面.(值得说明的是,解析延拓是一种非常强的约束.如果一个函数存在解析延拓,那么解析延拓的结果是唯一的. 在这里(s)的解析延拓刚好展现出了仿佛对称的样式,而不是先做了一个对称然后把它称为
具有相等大小的各阶谐波分量,因而当 被 调制以后, 的频谱就被调制到 的各阶谐波上,出现基带的频谱搬移. 正是这些频谱的总合.
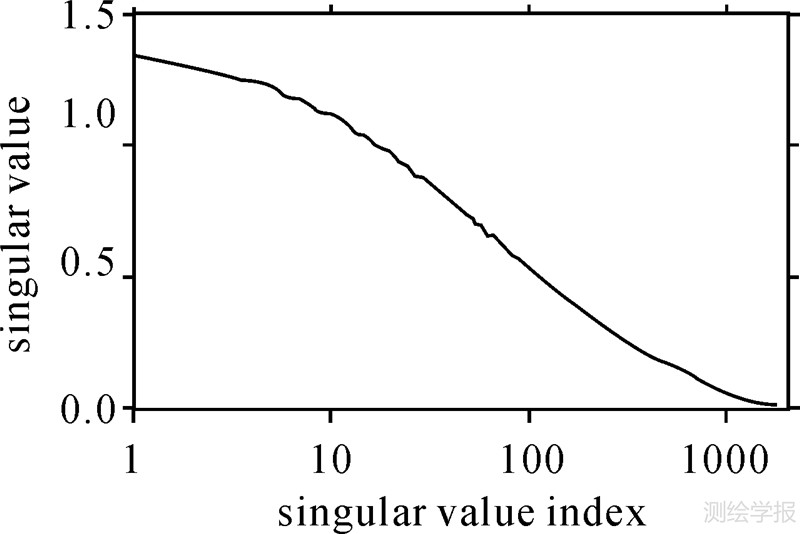
如上所述,向下延拓问题的法矩阵一般呈现出病态性特征,其条件数往往远超病态临界值1000.经计算,由该区域数据组成的法矩阵条件数高达13328,属高度病态矩阵,若直接采用最小二乘方法(LS)求解,将造成结果的极不稳定.系数阵的奇异值分布情况如 所示.
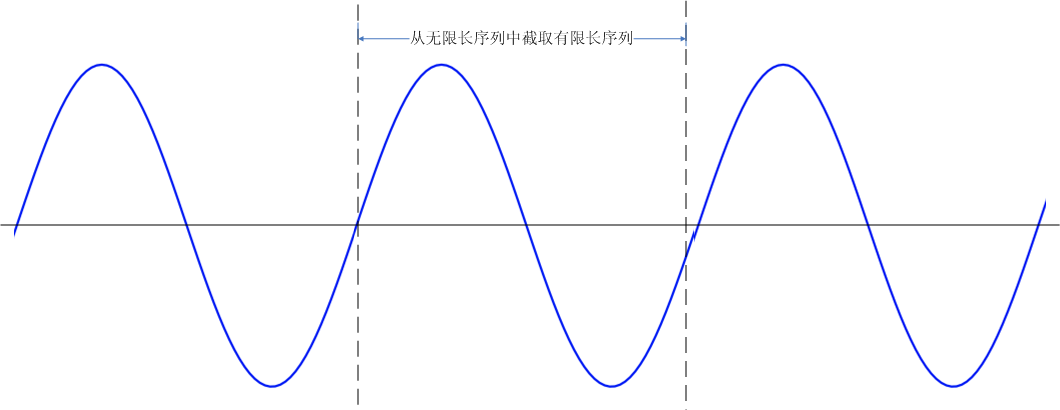
图1.从无限长序列中截取有限长序列 图1所示为无限长周期信号,我们截取了其中一段(有限长序列),这一段不是一个完整周期.傅里叶变换仍然将信号当成无限长序列,傅里叶变换又是如何将其当成无限长呢? 这里采用了一种被称为周期延拓的技术,所谓周期延拓,就是

每一月是一个小轮回,每一年则是一个大轮回,在上一次活动中未完成兑换的活动道具,若是积累到下一次同类型活动中使用,势必让你赚的满盆钵体;相信在天梯赛排行榜前列霸榜的大神们,有不少已经感受过此类收藏的魅力了. 特别的,诸如精灵精华这样几乎每次活动中都会遇上
非周期离散序列也是同样的求解思路. 将x[n]以N为周期延拓为x~[n],它们在±N的区间内是相等的. 写出x~[n]的傅里叶级数: 根据x~[n]和x[n]的关系,ak可以写为(求和中的N->∞): 设后面的求和公式为X(jw): 它
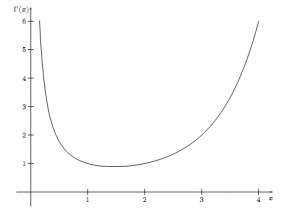
Gamma 函数找到了,我们来看看第二个问题,为何 Gamma 函数被定义为 $\\Gamma(n)=(n-1)!$, 这看起来挺别扭的.如果我们稍微修正一下,把Gamma 函数定义中的 $t^{x-1}$ 替换为$t^x$ 于是,利用上式把阶乘延拓到实

版本延拓,奇迹长青,《全民奇迹MU》上演轮回的奥义!如果你没有清空背包的强迫症,不妨也来做一个眼光长远的奇迹收藏家吧! 关于《全民奇迹MU》: 《全民奇迹MU》是一款获得韩国网禅十年经典网游《奇迹MU》正版授权的3D动作类RPG多人在线手游,由北京


版本延拓,奇迹长青,《全民奇迹MU》上演轮回的奥义!如果你没有清空背包的强迫症,不妨也来做一个眼光长远的奇迹收藏家吧! 每一月是一个小轮回,每一年则是一个大轮回,在上一次活动中未完成兑换的活动道具,若是积累到下一次同类型活动中使用,势必让你赚的满盆钵体

追问: 公式一样,为什么不是一部分? 追答: 是的,按如上不同的方式得到的傅立叶级数可以是不同的.如按周期偶延拓展开成的傅立叶级数是余弦级数;按周期奇延拓展开成的傅立叶级数是正弦级数;而按一般的周期延拓则展开成兼有正弦项和余弦项的傅立叶级数.但

堆叠数激增,背包仓库再升级 其实,随着《全民奇迹MU》版本不断更迭,玩家朋友们的这一情况早已不再称之为烦恼.在资源道具堆叠数从99提升到999,进而向9999飞跃的同时,勇士们背包与仓库的空间格子,也再进一步增大,只要达到一定的在线时长,就能将其陆续开
网友:李琼棠:只能勉强住住。
网友:陈仪生: 原来霄焰心里早有了别人!阿婉听完男子的话,心里反倒好受许多。
网友:金松:一掌将小茹推开,躲过了钢刀。
网友:薛编弼: 听到对方的话,秋道丁次直接说道:“我们是不会告诉你鸣人在哪里的!”
网友:于婆:
网友:董福嶂:“你当年努力过,如今却不想努力了,我说的没错吧。
网友:吴话偿:我是持有保留意见的,我认为到时候最有可能的结果,就是佐助被晓组织的那个宇智波一族的人利用,把自己原本对鼬的仇恨,以及杀死了鼬的悔恨,一起转嫁到了木叶的头上,乃至于世界的头上。
网友:胡臣:灵魂强度颇为有限。
- 上一篇:中职语文 中职语文试卷及答案_中职语文下册试卷及答案
- 下一篇:返回列表




