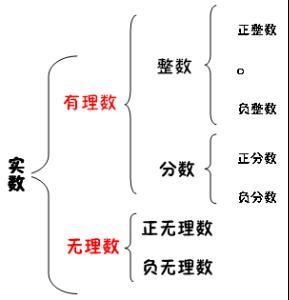
基本概念 实数 包括有理数和无理数.其中无理数就是 无限不循环小数 (二)确实的数字.【例】公司到底还有多少钱?请你 告诉我 实数

实数的运算 实数包括有理数和无理数.其中无理数就是无限不循环小数,有理数就包括整数和分数.数学上,实数直观地定义为和数轴上的点一一对应的数.本来实数仅称作数,后来引入了虚数概念,原本的数称作\"实数\"--意义是\"实在的数\". 实数的相关概念以及实数的

拓展资料: 实数,是有理数和无理数的总称.数学上,实数定义为与数轴上的点相对应的数.实数可以直观地看作有限小数与无限小数,实数和数轴上的点一一对应.但仅仅以列举的方式不能描述实数的整体.实数和虚数共同构成复数. 实数包括有理数和无理数.其中无理数就

扩展资料: 数学上,有理数是一个整数a和一个正整数b的比,例如3/8,通则为a/b.0也是有理数.有理数的小数部分是有限或为无限循环的数. 与有理数相对的是无理数.不是有理数的实数称为无理数,即无理数的小数部分是无限不循环的数.它不能写作两整数之比

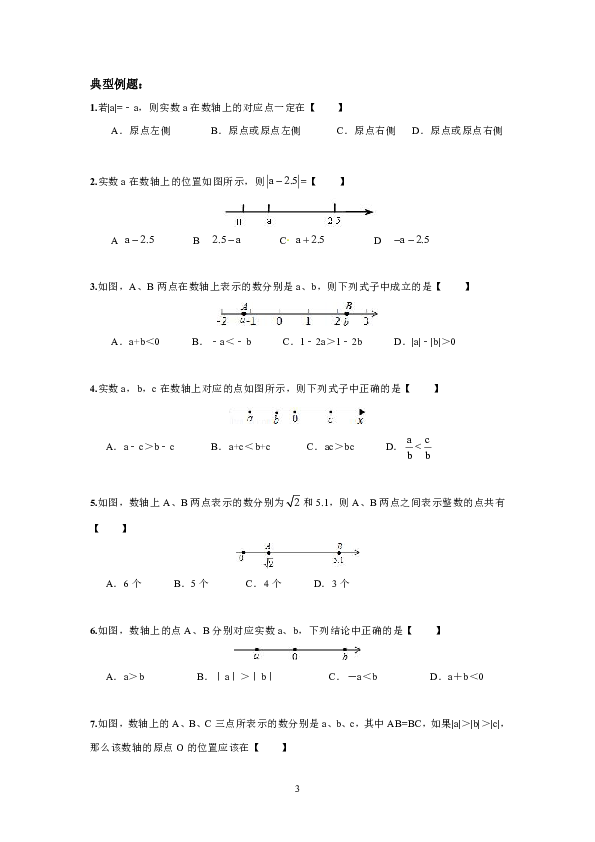
==================资料简介======================从本讲开始,我们针对中考数学中的热门考点,从数学的基础知识方面分26个专题进行探讨. 实数的概念和计算,是每年中考的必考内容之一,考查的知识点包括实数的概念和实数的计算
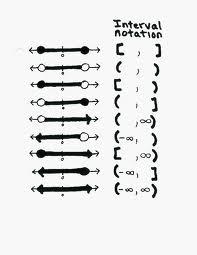
在数学里,区间通常是指这样的一类实数集合:如果x和y是两个在集合里的数,那麽,任何x和y之间的数也属于该集合.例如,由符合0≤x≤1的实数所构成的集合,便是一个区间,它包含了0、1,还有0和1之间的全体实数.其他例子包括:实数集,负实数组成的集合等.区间在

扩展资料: 实数可以用通过收敛于一个唯一实数的十进制或二进制展开.如 所定义的序列的方式而构造为有理数的补全.实数可以不同方式从有理数构造出来.这里给出公理的方法. 设 R 是所有实数的集合,则: Ⅰ 集合 是一个域: 可以作加、减、乘

解:由题意知本题是一个等可能事件的概率, ∵试验发生包含的事件是在区间[-2,2]上任取两个数a和b, 事件对应的集合是Ω={(a,b)|-2≤a≤2,-2≤b≤2} 对应的面积是sΩ=16, 满足条件的事件是关于x的方程x2-ax+b2=
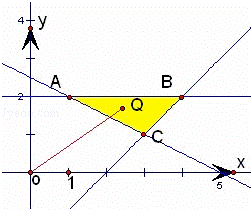
则目标函数 则 的取值范围是 故选C. 巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.本题主要考查了简单的线性规划,以及利用几何意义求最值,
第6章实数 专项训练2(含答案) 第6章 实数 专项训练专训1 巧用实数及相关概念的定义解题名师点金:实数部分的内容主要包括有理数、无理数以及它们的相反数、倒数、绝对值的意义及性质.在实数范围内,相反数、倒数、绝对值的意义和在有理数范围内完全相同.21
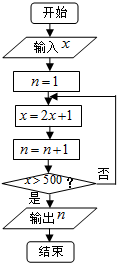
根据程序框图,若输入的实数x=1,则输出的n的值为( ) 题目列表(包括答案和解析)

在坐标轴上,作等腰直角△OMN,边OM=ON=1,则MN=√2,然后以O为圆心,以MN长为半径画弧,在x轴正方向截取OA=MN,则:A点在数轴上所表示的数就是无理数√2 数轴表示实数,实数包括有理数和无理数.因此无理数也可在数轴上表示出了.例如,在数轴
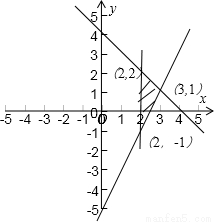
解:由题意,不等式组 ,表示一个三角形区域(包含边界),三角形的三个顶点的坐标分别为(2,2),(2,-1),(3,1) 目标函数z=3x+y的几何意义是直线的纵截距 由线性规划知识可得,在点(3,1)处取得最大值10. 目标函数z=3x+

离散椭圆曲线 上面的讲解中,我们看到椭圆曲线是条连续的曲线,之所以连续,是因为我们是在实数范围内取值的,也就是说曲线上各个点的横坐标和纵坐标都是实数. 可是,如果要把椭圆曲线应用于加密,是不能用实数的.因为实数包括了整数和小数,而小数不仅会让计算速

文件的第1行包含一个整数n和一个实数alpha,表示柠檬树的层数和月亮的光线与地面夹角(单位为弧度). 第2行包含n+1个实数h0,h1,h2,…,hn,表示树离地的高度和每层的高度. 第3行包含n个实数r1,r2,…,rn,表示柠檬树每层下底面的圆的半径
网友:郝驷哗:她狠拍着桌子站了起来。
网友:贾锆:看见白衣人的时候,突然脸色大变,神情阴晴不定,似乎在思索什么。
网友:孙嫡轮:沉『吟』片刻才缓缓说道。
网友:刘劬逮: 火遁,灰积烧!
网友:徐尉楼:眼睛瞪的溜圆。
网友:赵佛: 猿猴大吼一声,瞬间便动了起来。
网友:李滇邀:一声惨叫突然突然响起,只见一个暗部的忍者倒在了地面上,露出的皮肤迅速化为了深紫色,看起来是被某种毒素所侵入了身体,并且在微微抽搐之后,便失去了反抗的力量,死于非命。
- 上一篇:超级抽奖人生 都市大抽奖_诸天抽奖系统
- 下一篇:返回列表


