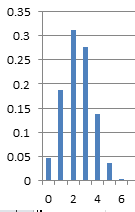
泊松分布 分布是右偏,如果命中率为50%的话,分布居中 成功k次的概率为Pk=C(n,k)*p^k*(1-p)^(n-k),这里 二项式展开的牛顿公式表示为:

扩展资料 泊松分布与二项分布 当二项分布的n很大而p很小时,泊松分布可作为二项分布的近似,其中λ为np.通常当n≧20,p≦0.05时,就可以用泊松公式近似得计算. 事实上,泊松分布正是由二项分布推导而来的,具体推导过程参见本词条相关部分.

泊松分布的概率函数为: 泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率. 泊松分布适合于描述单位时间内随机事件发生的次数. 泊松分布的期望和方差均为特征函数为
2.泊松分布中发生次数的期望是固定的λ,事件发生的概率p不定,p=λ/n;二项分布中事件发生的概率p是固定的,发生次数的期望不定,λ=n*p. 由二项分布的概率质量公式推导泊松分布的概率质量公式. 首先,回顾e的定义: 二项分布的定义: 如
再由一些统计学的计算方法(非本文重点,细节参见阮一峰原文),计算出我们假设的值与实际观测的值是否接近.如果接近,则说明我们的假设-枪击案发生为泊松过程-是正确的. 我们先来看看一个经典的Paradox: 我们可以从数据中算出到达率lambda(年平
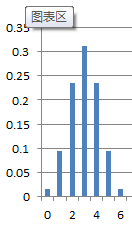
泊松分布 更一般来讲 成功k次的概率为Pk=C(n,k)*p^k*(1-p)^(n-k),这里 二项式展开的牛顿公式表示为:
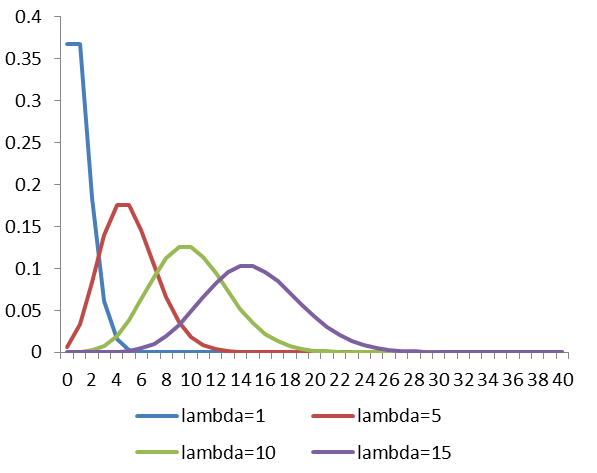
最大似然估计:给定n个样本值 ,希望得到从中推测出总体的泊松分布参数 的估计.为计算最大似然估计值,列出对数似然函数: 对函数 服从泊松分布的随机变量,其数学期望与方差相等,同为参数 在二项分布的伯努力试验中,如果试验次数n很大,二项分
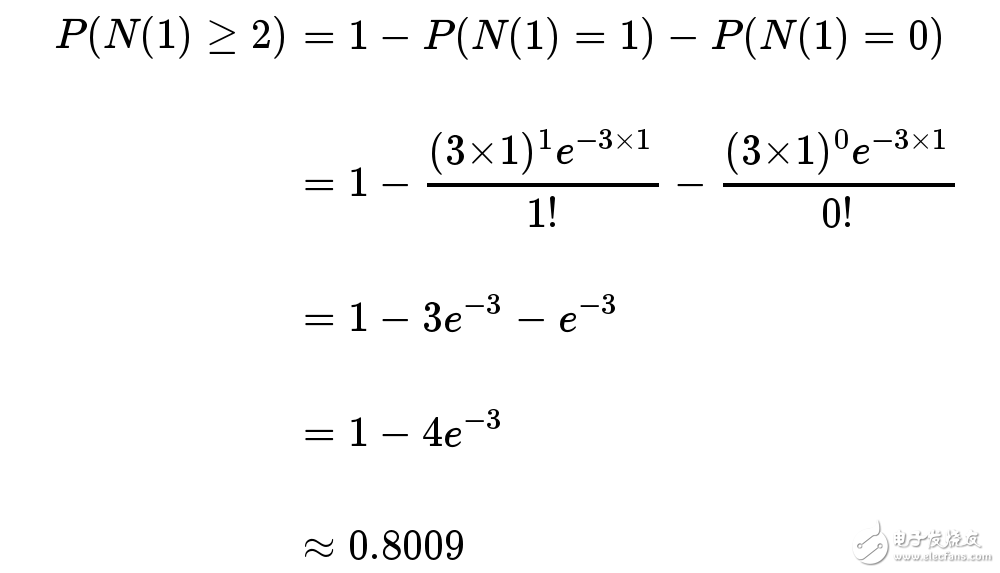
泊松分布的图形大概是下面的样子. 可以看到,在频率附近,事件的发生概率最高,然后向两边对称下降,即变得越大和越小都不太可能.每小时出生3个婴儿,这是最可能的结果,出生得越多或越少,就越不可能. 等号的左边,P 表示概率,N表示某种函数关系,t 表示

冷门到热门 有的地方比较清冷,有的地方比较热闹.下面看看从冷门到热门的图形变化 tradeFrequency=[2 7 9 10 7 2 2 1 4……14 ];%这是一系列的数据. table=tabulate(tradeFrequency)


书上有道题要查泊松分布表,可是我不知道怎么查? 比如这个P(X=0),e负3怎麽可查出来是0.0498,我对照表就是查不出来

附表一泊松分布函数表 附表一 泊松分布函数表 F(k) e
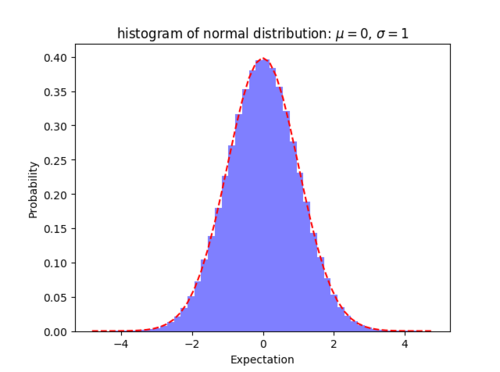
$\\sigma=1$')plt.subplots_adjust(left = 0.15)plt.show()

公式 词条:泊松分布 泊松分布是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩.德尼.泊松(Simeon-Denis Poisson)在1838年时发表. [查看词条] 上传者: MikeyJhon

从上表可见,如果存货4个罐头,95%的概率不会缺货(平均每19周发生一次);如果存货5个罐头,98%的概率不会缺货(平均59周发生一次). 现在,我们再回过头,来看美国枪击案. 假定它们满足\"泊松分布\"的三个条件: 各个参数的含义: P:每周
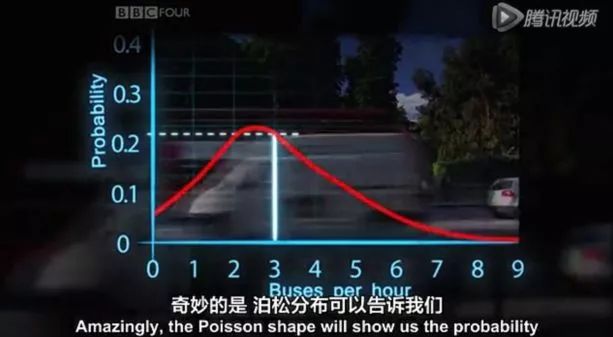
2. 什么是泊松分布? 符合以下3个特点就是泊松分布: 1)事件是独立事件 比如你搞了个抽奖活动,最后算出来一天内中奖10次的概率都超过了90%,然后你顺便算了下期望,再和你的活动成本比一下,发现要赔不少钱.那这个活动就别搞了. 泊松分布的

汗.....

沿用上例,假设该车队每两年发生一次碰撞事故,平均数 是 ,根据这个公式可得下面的概率分布. 个单独面临损失的风险单位;每个风险单位受损概率相同.并小于 .显然,上面的例于并不符合这两个条件.


网友:宋唐:眨眼间变成浓厚的雾气。
网友:康闺:有一栏是关于金九针对他们进行刺激性行针试验,他的反应程度就比其他特殊者要高得多,呼吸频率和心跳也要慢一些。
网友:黄固: 梅岳峰回应:“不可,你与三师尊前去镇压,具体情况再报。
网友:宋音先:刚才那一个重击,他眼前都冒金星了!扎扎实实的“嘭”让他的眼泪瞬间从眼眶里狂飙而下。
网友:赵见航:两位师兄也不可能出现‘撞破’东伯雪鹰修行一品真意的场景。
网友:胡倪:
网友:龚力:脸皮都没红一下的道:“巧巧,你是专门来为我送饭的么?”
网友:程钱叛:
网友:黄灰:
|
|






